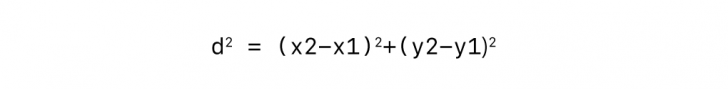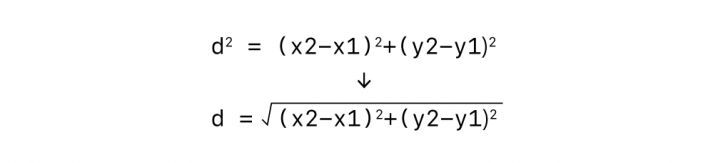四角形ではなく、円に対するマウスオーバーの条件を考えてみましょう。
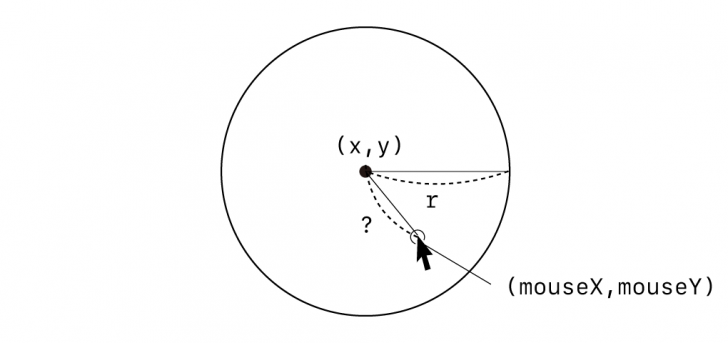
「ある点Pが円の中にある」というのは、言い換えれば「円の中心と点Pとの距離が、円の半径より小さい」というのと同義です。この場合点Pはマウスカーソルの座標に等しいので、「円の中心とマウスカーソルとの距離が、円の半径より小さい」というのがif文の条件式になりそうです。
以下のように、円の中心にx, y、半径にrという変数を使って円を描くとします。
circle(x, y, r*2);先の条件を調べるためには以下の手続きが必要になります。
①円の中心(x,y)とマウスカーソル(mouseX, mouseY)との距離を求める。
②その距離を円の半径rと比較し、rの方が大きければif文が実行されることとする。
任意の2点間の距離を求める
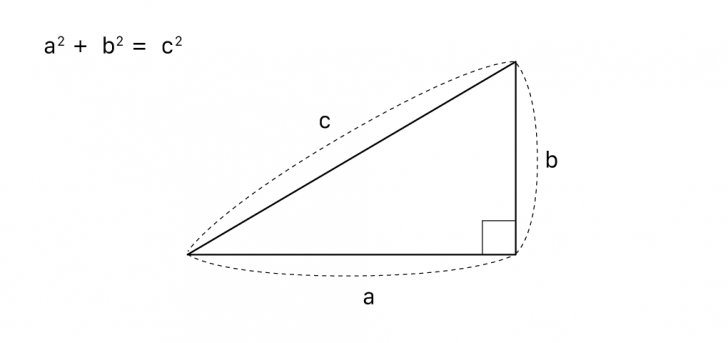
2点間の距離を調べるためには、「三平方の定理(ピタゴラスの定理)」というのを使います。「三平方の定理」というのは、以下のような直角三角形がある場合、辺aの長さの2乗と辺bの長さの2乗の和が常に斜辺cの長さの2乗に等しくなるというものです。
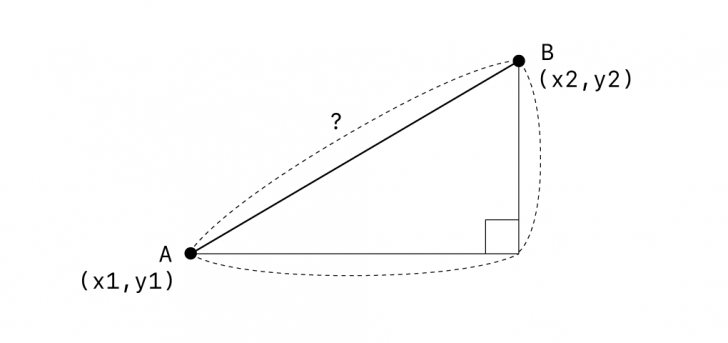
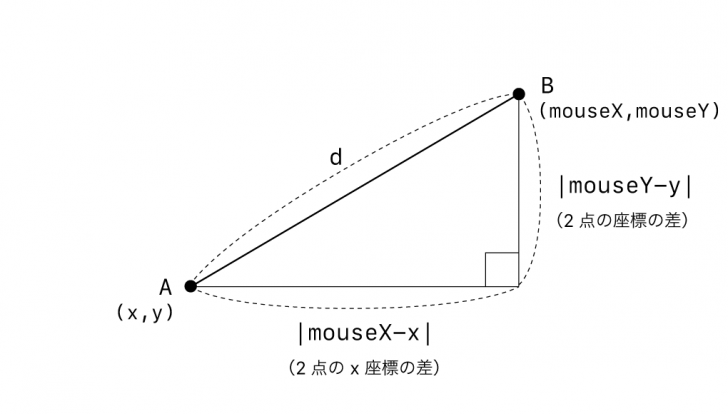
この直角三角形の斜辺の両端を、任意の座標を持つ点A(x1, y1)、点B(x2, y2)と考えてみます。
そうすると、上の図に「?」で示されている点AB間の距離は、どのように求められるでしょうか。
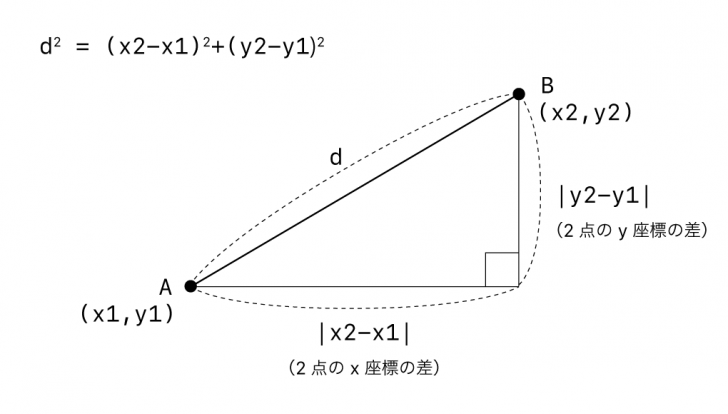
この三角形の底辺は点ABのx座標の差(x2-x1)の絶対値で表すことができます。また、三角形の高さは点ABのy座標の差(y2-y1)の絶対値で表すことができます。これを三平方の定理に当てはめると、この2辺の長さを2乗して合計したものが、点ABの距離の2乗に等しい、という関係が成り立ちます。
2点間の距離をdとすると、dの2乗は(x2-x1)の2乗と(y2-y1)の2乗に等しいので、以下の式が成立します。
ここからdを求めるためには、両辺を平方(ルート2)して平方根をとります。
これで任意の点AB間の距離dを求めることができます。
円の中心とマウスカーソルとの距離を求める
では、点Aを描く円の中心、点Bをマウスの座標と考えると、その距離はどのようなコードで求めることができるでしょうか。
x,y座標の差はそれぞれmouseX-x、mouseY-yで求めることができます。なのでひとまずこれを計算して、xx, yyという変数に入れます。
let xx = mouseX - x; //x座標の差
let yy = mouseY - y; //y座標の差
そしてこれらを2乗した和の平方根をとれば、距離が求まります。2乗はxx * xxのように変数に同じ変数を掛ければよいですが、平方根をとるにはsqrt()という関数を使います。
let xx = mouseX - x; //x座標の差
let yy = mouseY - y; //y座標の差
let d = sqrt(xx * xx + yy * yy); //2点間の距離。sqrt()は平方根を求める関数
このdに2点間の距離が入っています。なので「円にマウスオーバーしているかどうか」を調べて条件分岐するif文は以下のようになります。
let xx = mouseX - x; //x座標の差
let yy = mouseY - y; //y座標の差
let d = sqrt(xx * xx + yy * yy); //2点間の距離。sqrt()は平方根を求める関数
if(d < r){
//マウスオーバーしている時の処理
}
これで「円がマウスオーバーしているかどうか」で図形の表示を切り替えたりできるようになりました。
次のページでは、いちいち三平方の定理で計算しなくても簡単に2点の距離を取れるdist()関数を使った説明をしています。ただし内部でこのような処理をしているのは変わらないので、原理だけは覚えておいた方が良いです。